-
- 品质管理规划资料分享
- 七手法之柏拉图制作详细步骤培训资料
- QC七大工具绘制方法培训资料
-
在Boss协会学习六西格玛合集-持续更新
绝对是精品教程了,认真学习能够达到一个不错的层次,对六西格玛认知提高了很多很多,谢谢分享!
- 22年毕业后的安全人都怎么样了
-
SPC&CPK-EXCEL模板分享
该模板是一套以Excel®为载体的统计过程控制(SPC)与制程能力(Capability Study)集成工具,覆盖计量型与计数型全部常用控制图,并内嵌完整CPK/PPK计算逻辑,可直接用于IATF 16949、VDA 6.3、ISO 22514-2等体系的新产品导入(APQP-PPAP)、过程稽核及量产监控。 计量型控制图 ① Xbar-R Chart(n≤8) - 自动调用d2、D3、D4常数,实时计算UCLR、LCLR、UCLX̄、LCLX̄ - 采用Nelson 8大判异规则,异常点条件格式高亮 - 同步输出组内标准差σ̂=R̄/d2,用于CPK公式计算 ② Xbar-S Chart(n≥9) - 以c4修正样本标准差,降低方差估计偏倚 - 提供B3、B4系数,自动生成UCLS、LCLS ③ X-MR Chart(n=1) - 移动极差MR=|Xi-Xi-1|,E2系数计算控制限 - 适用于破坏性、成本高昂或低频采样场景 计数型控制图 ④ p Chart / np Chart - 支持变样本量与固定样本量双模式 - 控制限采用3σ泊松-正态近似,自动处理过度离散(Over-dispersion) ⑤ c Chart / u Chart - 缺陷数与单位缺陷数模型,内置√c及√u变换 - 提供Laney u’修正选项,适配大样本、多缺陷场景 制程能力分析(Capability Study) ⑥ CPK/PPK集成工作表 - 指标算法完全依照AIAG SPC-2与ISO 22514-2: CP=(USL-LSL)/6σ̂short PP=(USL-LSL)/6σ̂long CPU=(USL-X̄)/3σ̂short CPL=(X̄-LSL)/3σ̂short CPK=Min(CPU,CPL) PPK=Min(PPU,PPL) - 同步输出Ca(准确度)与PPM预估(基于Z-score正态尾部面积) - 自动评定Grade A~D,并提示目标CPK≥1.67或1.33的符合性 辅助工具 ⑦ 正态分布累积函数表(z-table) - 覆盖z=[0,4]区间,步长0.01,可直接读取单侧/双侧PPM ⑧ 控制图选用决策树 - 按数据类型、样本容量、采集方式三维度快速定位最佳控制图 ⑨ 组距直方图与Normal Probability Plot - 采用Sturges与Freedman-Diaconis双准则优化组距 - 内置Ryan-Joiner正态性检验p-value估算,减少Minitab依赖 三、技术架构与质量保障 公式层:所有计算单元格均锁定,采用Excel LET与LAMBDA动态数组,防止误删 图表层:控制图与直方图基于动态命名范围(OFFSET+INDEX),新增数据自动扩展 验证层:关键结果(CPK、UCL、LCL)与Minitab® 21、JMP® 17交叉验证,误差<1‰ 合规层:指标符号、公差表达、判异规则与AIAG SPC-2第四版、JIS B 9704:2021完全一致 四、典型应用场景 APQP阶段 • 初始过程能力研究(PPAP Level 3提交) • 快速确认关键特性SC/CC是否达成CPK≥1.67 量产监控 • 自动刷新Daily SPC报告,邮件推送异常Alarm • 结合Shopfloor MES,实现Excel前端+SQL后端轻量级SPC系统 供应商质量审核 • 现场打开模板即可展示实时控制图与能力指数,减少稽核时间50 % 五、使用须知 启用宏:部分按钮需启用Office宏以触发自动刷新 数据格式:计量型数据建议保留6位小数,避免舍入误差放大CPK偏差 过程稳定性:计算CPK前须先通过Xbar-R或Xbar-S图确认过程处于统计控制状态(无Nelson规则报警) 双边规格缺失:若仅单边USL或LSL,模板自动切换单边能力指数CPU或CPL,并屏蔽CPK显示 将“SPC控制图绘制→稳定性判定→CPK公式计算→PPM预估→报告输出”全流程封装为免代码、零插件的Excel环境解决方案,是质量工程师、工艺工程师及供应链管理人员快速落地IATF要求、建立数据驱动过程控制体系的实用利器。
- SPC&CPK-EXCEL模板分享
-
cpk计算公式及其背后的每一个知识点
一、CPK 是什么?CPK(Process Capability Index,过程能力指数) 是衡量一个过程满足产品质量标准(规格)能力的数值指标。它告诉我们,我们的生产过程是否稳定,并且能否持续地生产出符合规格要求的产品。 核心思想: 将过程的自然波动范围(基于实际数据)与客户允许的规格范围进行比较。 CPK值高(通常 > 1.33):说明过程的自然波动远小于规格范围,过程能力强,产生不合格品的风险极低。 CPK值低(通常 < 1.0):说明过程的自然波动已经接近甚至超过了规格范围,过程能力弱,有很大风险产生不合格品。 二、CPK 的计算公式CPK 的计算公式有两个,取其中较小的那个值作为最终的CPK。 公式 1:关注上限规格 Cpu = (USL - μ) / 3σ 公式 2:关注下限规格 Cpl = (μ - LSL) / 3σ 最终的 CPK: CPK = Min(Cpu, Cpl) 为什么取最小值? 因为过程的能力取决于它最薄弱的那一环。好比一个木桶能装多少水,取决于最短的那块木板。 三、公式中每个知识点的详细讲解让我们来逐一拆解公式中的每一个符号和概念。 1. USL 与 LSL(规格上下限)USL(Upper Specification Limit):规格上限。客户或标准允许的最大值。超过这个值,产品就不合格。 例子:一个轴的长度,客户要求最大不能超过10.05mm。 LSL(Lower Specification Limit):规格下限。客户或标准允许的最小值。低于这个值,产品也不合格。 例子:同一个轴的长度,客户要求最小不能短于9.95mm。 公差(Tolerance):USL - LSL 就是公差范围,代表了客户允许的总波动范围。 2. μ(过程均值)定义:过程输出数据的平均值。它代表了过程的“中心位置”。 计算:μ = (X1 + X2 + ... + Xn) / n (其中X1, X2...是单个测量值,n是样本数量) 重要性:理想情况下,过程均值 μ 应该与规格中心值 (USL + LSL)/2 重合。如果 μ 偏离了中心,即使过程波动很小,也会导致CPK值降低。 3. σ(过程标准差)定义:衡量过程输出数据的离散程度,即“波动”有多大。σ 是 CPK 计算中最关键的因素之一,因为它代表了过程的固有波动。 计算:对于样本数据,通常使用 σ = R̄ / d2 来估计。 R̄ 是子组极差(R)的平均值。极差 R = 子组内最大值 - 子组内最小值。 d2 是一个与子组大小相关的常数(例如,子组大小为5时,d2 ≈ 2.326)。 为什么用 3σ? 对于一个呈正态分布的过程,其数据会落在 μ ± 3σ 范围内的概率是99.73%。这意味着过程的自然波动范围(宽度) 大约是 6σ。 因此,3σ 可以看作是“过程自然波动范围的一半”。 4. Cpu 与 Cpl(单边过程能力)Cpu(上限过程能力指数): (USL - μ) 表示从过程中心到上限还有多少“空间”。 将这个空间除以 3σ(过程一半的自然波动),就得到了过程满足上限要求的能力。比值越大,说明空间越充裕,越不容易超上限。 Cpl(下限过程能力指数): (μ - LSL) 表示从过程中心到下限还有多少“空间”。 同样,除以 3σ 得到满足下限要求的能力。 四、CPK 计算的全过程示例场景: 加工一根轴,规格要求是 10.00 ± 0.05 mm。即 LSL = 9.95 mm, USL = 10.05 mm。 我们抽取了25组数据,每组5个样本(共125个数据)。经过计算: 过程均值 μ = 10.01 mm 平均极差 R̄ = 0.02 mm 子组大小 n=5,查表得 d2 = 2.326 计算步骤: 估算过程标准差 σ σ = R̄ / d2 = 0.02 / 2.326 ≈ 0.0086 mm 计算单边过程能力 Cpu = (USL - μ) / 3σ = (10.05 - 10.01) / (3 * 0.0086) ≈ 0.04 / 0.0258 ≈ 1.55 Cpl = (μ - LSL) / 3σ = (10.01 - 9.95) / (3 * 0.0086) ≈ 0.06 / 0.0258 ≈ 2.33 确定 CPK CPK = Min(1.55, 2.33) = 1.55 结果解读: 这个过程的CPK是1.55。由于它大于1.33,通常认为这个过程能力是充足的。但是,我们可以看到 Cpu (1.55) 远小于 Cpl (2.33),这是因为过程中心(10.01)更靠近上限(10.05),导致向上波动的“安全空间”较小。为了进一步提升CPK,我们应该首先考虑将过程均值 μ 调整到规格中心 10.00。 五、CPK 与 CP 的区别(非常重要!)CP(过程潜力指数): 公式:CP = (USL - LSL) / 6σ 含义:只关注过程的“潜在”能力,即过程的自然波动(6σ)与公差范围的对比。它不考虑过程中心 μ 的位置。 在上面的例子中:CP = (10.05 - 9.95) / (6 * 0.0086) ≈ 0.1 / 0.0516 ≈ 1.94。这个值很高,说明过程波动本身很小,潜力很大。 CPK 与 CP 的关系: 当过程中心 μ 正好位于规格中心时,CPK = CP。 当过程中心 μ 发生偏移时,CPK < CP。 CP 告诉我们过程“理论上”能做多好,而 CPK 告诉我们过程“实际上”做得怎么样。 CPK 是一个更现实、更严格的指标。 六、使用 CPK 的前提条件过程必须稳定(受控):需要使用控制图(如Xbar-R图)来确认过程没有异常波动。在一个不稳定的过程中计算CPK是没有意义的。 数据必须服从或近似服从正态分布:CPK的计算基于正态分布的假设。如果数据严重非正态,需要使用其他方法(如转换数据或使用非正态过程能力指数)。 概念 符号 含义 在CPK中的作用 规格上限 USL 客户允许的最大值 定义合格范围的边界 规格下限 LSL 客户允许的最小值 定义合格范围的边界 过程均值 μ 过程的中心位置 反映过程是否对准目标值 过程标准差 σ 过程的波动大小 衡量过程的固有变异,是核心 单边上限能力 Cpu 过程满足上限的能力 取两者中较小者,体现“短板效应” 单边下限能力 Cpl 过程满足下限的能力 取两者中较小者,体现“短板效应”
-
应届毕业生直接当品质主管?
我是过来人,算是你们做品质的老前辈了,我真心建议你要求老板请外部三方来进行培训,因为你们企业内部从来不知道这些,看资料是学不精的,在老板支持的情况下提升自己,老板不支持的情况下适当投资提升自己是很不错的选择。最后,一些杂活是可以找文员完成的,你可以想个适当的理由招一个文员。
-
cpk是什么意思,回答部分私信的朋友
CPK就像是一个“体检报告”,用来衡量一个生产过程(比如做蛋糕、造零件)的“健康程度”和“稳定性”。它的数值越高,说明生产过程越稳定,出废品的风险越低。 通俗简单的解释想象一下你在用模具做饼干: 目标:每个饼干都完美地符合模具的形状和尺寸(这叫规格中心)。 允许的误差:客户允许饼干稍微大一点点或小一点点,但不能太大或太小,否则就是次品(这个允许的范围叫规格上下限)。 你实际做的:你不可能每个饼干都一模一样,总会有大有小(这些实际饼干尺寸的分布,叫过程能力)。 那么,CPK就是来回答一个问题: 你做的这些饼干,它们的尺寸波动范围,和客户允许的误差范围相比,到底有多“富裕”?或者说,你的生产过程有没有“撞到”客户允许的边界线上? CPK > 1.33:说明你的生产过程非常稳定,饼干的尺寸都稳稳地落在允许范围的正中央,离边界线很远,基本不会出次品。(优秀) CPK ≈ 1.0:说明你的生产过程刚好能满足要求,但已经有点“擦边”了,稍微一不稳定就可能出次品。(及格,但有风险) CPK < 1.0:说明你的生产过程不稳定,已经有一部分饼干超出了允许范围,正在生产次品!(不及格) 所以,工厂喜欢追求高CPK,因为这代表质量可靠、浪费少、成本低。 1. CPK本身的名称含义CPK这个名称由两部分组成: CP: 代表 Process Capability(过程能力指数)。 它只关注过程的波动与规格公差的比值。可以理解为过程的“潜在能力”。 计算公式:CP = (规格上限 - 规格下限) / (6 * 标准差) 它有一个缺陷:它假设过程输出的平均值正好在规格中心。如果过程中心偏移了,CP指数就不准了。 K: 代表 偏离系数(Correction Factor)。 这个K就是用来修正上面提到的“过程中心偏移”问题的。 所以,CPK = 修正后的过程能力指数。它的计算公式考虑了过程的平均值(μ)与规格中心(M)的偏移。 计算公式: CPK = min[ (规格上限 - 平均值) / (3 * 标准差), (平均值 - 规格下限) / (3 * 标准差) ] 为什么取最小值? 因为一个过程的短板在于它离哪个规格界限更近。CPK关心的是最危险的那一边,确保即使有偏移,也不会生产出不合格品。 2. CPK的来源与历史CPK的概念和统计过程控制(SPC)理论紧密相关,其奠基人是休哈特博士。 20世纪20年代:休哈特在贝尔实验室工作,为了改善工业生产过程的质量,他发明了控制图。控制图的核心思想是:任何过程都存在“正常波动”(由普通原因引起)和“异常波动”(由特殊原因引起)。管理的目标是消除异常波动,并将正常波动控制在一定范围内。 后续发展:在休哈特控制理论的基础上,后来的质量管理和统计学家们为了更量化地衡量一个过程在“仅受正常波动影响”下的潜在表现,发展出了“过程能力”的概念。 CPK的诞生:最初的CP指数假设过程是无偏的,但这在实际生产中很难做到。为了解决这个实际问题,引入了考虑中心偏移的修正指数,即CPK。它成为了衡量“实际过程能力”的更准确、更实用的指标。 3. CPK在工业中的应用CPK是六西格玛管理和质量管理体系中的核心统计工具。它主要用于: 新过程/新设备的验收:评估其是否具备生产合格产品的能力。 过程的持续监控:定期计算CPK,发现过程变差的趋势,提前预警。 供应商评估:评估供应商的生产保证能力。 减少变异:通过提高CPK,推动企业减少生产过程中的波动,提升产品质量和一致性。 CPK是什么:CPK是衡量过程稳定性和满足规格能力的指数。 名字由来:C(过程能力) + P + K(修正系数) = 修正后的过程能力指数。 核心思想:它不仅看过程的波动有多大,还看这个过程波动的位置有没有“跑偏”。 来源:源自休哈特的统计过程控制理论,是质量管理科学发展的重要成果。
-
质量战略培训pdf资料分享
质量战略培训pdf资料分享 为什么要培训质量战略? 培训质量战略的根本原因在于,它能让企业从被动“救火”转向主动“防火”。在激烈市场竞争中,质量不再是单一的产品合格,而是关乎品牌声誉、客户忠诚度和运营效率的核心竞争力。通过培训,管理层能意识到质量是战略投资,而非成本负担。它能统一全员思想,将质量目标与业务目标对齐,从而系统性降低内外部失败成本,提升整体效益,实现可持续发展。 什么是质量战略培训? 质量战略培训是一套系统的学习过程,旨在教导组织(尤其是管理层)如何制定、部署和实施旨在获得长期竞争优势的质量方针和目标。它超越了基础的质量控制工具,重点在于: 思想转变:树立“第一次就把事情做对”的预防性质量文化。 战略制定:学习如何将客户需求转化为可衡量的质量目标,并整合到企业战略中。 体系搭建:指导如何构建高效的质量管理体系,确保流程最优、资源分配合理。 领导力提升:培养管理者驱动变革、引领全员持续改进的能力。
- 质量战略培训资料分享
-
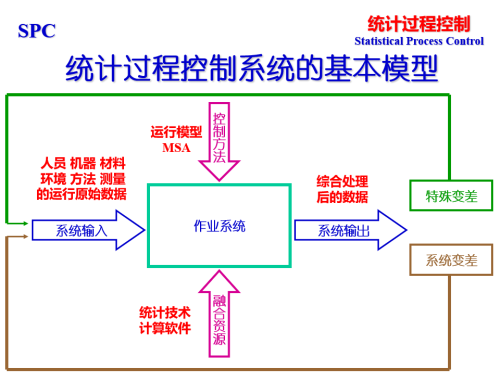
SPC统计过程控制培训学习资料_超详细讲解
为什么要进行SPC统计过程控制培训? SPC统计过程控制培训的核心目的,是让企业从“事后检验”转向“事前预防”,实现质量管理的飞跃。其必要性体现在: 首先,它能降本增效。通过培训,员工学会利用控制图等工具实时监控生产过程,能及时发现异常趋势并纠正,大幅减少不良品和返工,直接降低质量成本和物料浪费,提升生产效率和效益。 其次,它为企业提供科学决策依据。SPC用数据说话,改变了凭经验“拍板”的旧模式。管理者可以基于客观数据,准确判断过程能力、评估改进效果,使决策更精准、更科学。 再者,它有助于建立持续改进的文化。培训让全员掌握共同的质量语言和改进方法,将质量控制从质检部门的责任转变为全员的自觉行动,为企业推行精益生产、六西格玛等奠定坚实基础,从而系统性地提升核心竞争力。 SPC培训是企业追求卓越质量、实现可持续发展的关键投资。 注册或登陆Boss协会可免费下载!
-
SPC Statistical Process Control:SPC统计过程控制培训学习资料_超详细讲解
-
六西格玛cpk计算公式详解-超级详细
1. Cpk 的核心概念与目的Cpk(过程能力指数)是衡量一个稳定的生产过程能够满足规格要求(例如,客户要求的公差范围)程度的指标。它的核心价值在于: 同时考虑过程的集中趋势(平均值)和离散程度(标准差)。这与只考虑离散程度的 Cp 指数不同。 评估过程“是否对准了目标值”。即使过程的波动很小(Cp很高),但如果平均值偏离了规格中心,Cpk也会变低。 Cpk 值越高,表示过程生产出不合格品的概率越低。通常,Cpk ≥ 1.33 被认为是过程能力良好的基准,而六西格玛水平追求的是 Cpk ≥ 2.0。 2. Cpk 的计算公式Cpk 的计算公式有两个,取其中较小的值作为最终的 Cpk。 公式 1:关注上限规格 Cpu = (USL - μ) / (3σ) 公式 2:关注下限规格 Cpl = (μ - LSL) / (3σ) 最终的 Cpk Cpk = min(Cpu, Cpl) 其中: min() 是取最小值的函数。这意味着过程的整体能力由其“更差的那一侧”决定,遵循木桶原理。 3. 公式中每个变量的详细解释让我们逐一拆解公式中的每一个符号。 μ - 过程平均值含义:过程输出数据的算术平均值。它代表了过程输出的中心位置或集中趋势。 计算方式:μ = (X₁ + X₂ + ... + Xₙ) / n X₁, X₂, ..., Xₙ 是从过程中收集的单个测量值(样本数据)。 n 是样本的总数量。 在公式中的作用: 在 Cpu 中,(USL - μ) 衡量的是过程平均值距离上限规格还有多远。这个距离越大越好。 在 Cpl 中,(μ - LSL) 衡量的是过程平均值距离下限规格还有多远。这个距离也是越大越好。 关键点:理想情况下,μ 应该与规格中心值 (USL + LSL)/2 完全重合。如果 μ 偏离中心,即使 σ 很小,Cpk 也会降低。 σ - 过程标准差含义:衡量过程输出数据的离散程度或波动大小。σ 值越小,说明过程越稳定,生产出的产品特性越一致。 计算方式:对于长期过程能力(Ppk 中使用),通常使用样本标准差: σ = √[ Σ(Xi - μ)² / (n - 1) ] Xi 是每个样本的测量值。 μ 是样本平均值。 n 是样本数量。 Σ 是求和符号。 在短期过程能力(Cpk)研究中,通常使用子组内标准差,最常用的是通过极差平均值来估计: σ = R̄ / d₂ R̄ 是所有子组极差(R = 子组内最大值 - 最小值)的平均值。 d₂ 是一个与子组大小相关的常数(例如,子组大小为5时,d₂ ≈ 2.326)。 在公式中的作用:3σ 代表了过程自然波动的范围。在正态分布下,99.73%的数据会落在 μ ± 3σ 的范围内。分母中的 3σ 实际上是将过程的“自然公差”与“规格公差”进行比较。 USL - 上限规格限含义:客户或工艺要求允许的最大值。超过这个值的产品即为不合格品。 示例:一个轴的直径要求是 10±0.1mm,那么 USL = 10.1mm。 LSL - 下限规格限含义:客户或工艺要求允许的最小值。低于这个值的产品即为不合格品。 示例:一个轴的直径要求是 10±0.1mm,那么 LSL = 9.9mm。 3 - 常数“3”含义:这个“3”代表了在计算中我们使用的是 ±3σ 的范围,即过程的“自然公差带”。这对应了正态分布下 99.73% 的覆盖率。在六西格玛方法论中,有时会使用“6”(即 ±6σ),但那是在计算 Sigma Level(西格玛水平)时,而不是计算传统的 Cpk。Cpk 的标准定义始终使用 3σ。 4. 公式的几何意义与图解想象一个正态分布曲线(钟形曲线): 规格中心:USL 和 LSL 中间的点。 过程中心:曲线的峰值,对应 μ。 过程Spread(散布):曲线的“胖瘦”,对应 σ。曲线越瘦,σ 越小。 Cpk 的计算就是在问:过程的自然波动范围(μ ± 3σ)与规格界限(LSL 和 USL)重叠部分最少的那一边,还剩下多少空间? (USL - μ) 或 (μ - LSL) 是可用空间。 3σ 是过程自身占用的空间。 Cpk 就是“可用空间”与“占用空间”的比值。 这个比值越大,说明安全边际越大。 5. 计算实例场景: 加工一个轴,规格要求是 10.00 ± 0.05 mm。即 LSL = 9.95 mm, USL = 10.05 mm。 从生产过程中抽取样本,计算得出: 过程平均值 μ = 10.02 mm 过程标准差 σ = 0.01 mm 计算步骤: 计算 Cpu(关注上限): Cpu = (USL - μ) / (3σ) = (10.05 - 10.02) / (3 * 0.01) = 0.03 / 0.03 = 1.0 计算 Cpl(关注下限): Cpl = (μ - LSL) / (3σ) = (10.02 - 9.95) / (3 * 0.01) = 0.07 / 0.03 ≈ 2.33 确定 Cpk: Cpk = min(Cpu, Cpl) = min(1.0, 2.33) = 1.0 结果解读: 这个过程的能力指数 Cpk 为 1.0。虽然下半部分有充足的空间(Cpl=2.33),但由于过程平均值(10.02)偏向规格上限,导致上半部分的空间非常紧张(Cpu=1.0)。根据 Cpk=1.0,我们可以估算出大约 0.27% 的产品会超出上限规格(不合格)。这个过程急需调整,将平均值 μ 向规格中心(10.00)靠近。 6. Cpk 与 Cp 的关键区别这是一个非常重要的概念: Cp 指数:Cp = (USL - LSL) / (6σ) 它只关心过程的波动(σ)相对于规格公差的总宽度。 它不关心过程平均值 μ 的位置。 如果 Cp 很高但 Cpk 很低,说明过程潜力很好(波动小),但定位不准(平均值偏离中心)。 Cpk 指数: 它同时关心过程的波动(σ)和平均值的位置(μ)。 Cpk ≤ Cp 永远成立。只有当过程完美居中时,Cpk = Cp。 总结Cpk 是一个强大的统计工具,它通过一个简洁的数字综合反映了过程的精度(σ,标准差)和准度(μ,平均值)与客户要求(USL/LSL)的匹配程度。理解和计算 Cpk 是六西格玛管理中评估和改善过程性能的基础步骤。 还不够详细,要极致的详细,包含cp、ppk等等 好的,我们来进行一次关于过程能力指数的极致详细的、百科全书式的详解。这将涵盖 Cp、Cpk、Pp、Ppk 的每一个层面,包括其哲学思想、数学基础、应用场景和细微差别。 第一部分:核心概念与哲学基础1.1 目的与重要性过程能力指数是一组用于量化过程输出满足规格要求能力的统计指标。其核心价值在于: 从定性到定量:将“这个过程好不好”的主观判断,转化为一个可比较的、客观的数字。 预测性能:基于历史数据,预测过程在未来生产出不合格品的概率。 共通语言:为工程师、质量人员、管理人员和客户提供统一的沟通标准。 改进导向:通过分析指数的构成,指明过程改进的方向——是减小波动(降低σ)还是调整中心(移动μ)。 1.2 基本思想:规格 vs. 自然波动任何过程都存在波动。过程能力分析的核心思想是对比两个宽度: 规格公差(Voice of the Customer, VOC):客户允许的、产品特性可以变动的范围。即 USL - LSL。 过程波动(Voice of the Process, VOP):过程本身固有的、实际的输出变异范围。通常用 6σ 来表示,因为它涵盖了正态分布下99.73%的数据。 核心问题:过程的“自然波动”(VOP)是否能轻松地装在“规格要求”(VOC)这个盒子里? 第二部分:四大核心指数的定义与公式2.1 Cp(过程能力指数)公式: Cp = (USL - LSL) / 6σ_within 极致详解: 分子 (USL - LSL):规格宽度。代表了客户的“容忍空间”。这个值是由设计或客户决定的,是固定的。 分母 6σ_within:组内波动宽度。代表了过程的短期、固有的波动。这里的 σ_within 是关键。 σ_within 的计算:它通常由子组内部的变异来估计,排除了子组间的变异。最常用的方法是: σ_within = R̄ / d₂ 或 σ_within = S̄ / c₄ R̄:所有子组极差(R)的平均值。 d₂:一个与子组容量(n)相关的统计常数。例如,n=5时,d₂=2.326。 S̄:所有子组标准差(s)的平均值。 c₄:另一个与子组容量(n)相关的统计常数。 Cp的物理意义:它衡量的是过程的“潜在能力”。它假设过程均值μ正好位于规格中心,并且只关心过程的精度(波动大小)。 Cp的局限性:它完全忽略了过程均值的位置。一个Cp很高的过程,如果均值严重偏离中心,仍然会产生大量不合格品。 2.2 Cpk(过程性能指数)公式: Cpk = min( Cpu, Cpl ) Cpu = (USL - μ) / 3σ_within Cpl = (μ - LSL) / 3σ_within 极致详解: min() 函数:取最小值。这体现了“木桶原理”,过程的能力由其最薄弱、最接近规格限的一侧决定。 分子 (USL - μ) 或 (μ - LSL):这是从过程中心到最近一个规格限的“可用空间”或“安全边际”。 分母 3σ_within:这是过程分布中心到其自然界限(μ ± 3σ)的“一半的波动宽度”。 Cpk的物理意义:它衡量的是过程的“实际能力”。它同时考虑了过程的精度(σ_within,波动)和准度(μ,位置)。 与Cp的关系: Cpk ≤ Cp 永远成立。 只有当过程均值μ恰好位于规格中心时,Cpk = Cp。 当μ偏离中心时,Cpk 会小于 Cp。 2.3 Pp(过程性能指数)公式: Pp = (USL - LSL) / 6σ_overall 极致详解: 公式形式与Cp相同,但分母中的标准差有本质区别。 分母 6σ_overall:整体波动宽度。代表了过程的长期、总变异。它包含了所有来源的变异:组内变异、组间变异、时间推移带来的漂移等。 σ_overall 的计算:它使用所有个体数据(不分组)计算的标准差。 σ_overall = √[ Σ(Xi - μ)² / (N - 1) ] Xi:每一个单独的测量值。 μ:所有数据的总体平均值。 N:所有测量值的总个数。 Pp的物理意义:它衡量的是在长期情况下,过程输出的总变异相对于规格公差的对比。它反映了过程的“整体表现”。 2.4 Ppk(过程性能指数)公式: Ppk = min( Ppu, Ppl ) Ppu = (USL - μ) / 3σ_overall Ppl = (μ - LSL) / 3σ_overall 极致详解: 公式形式与Cpk相同,但同样使用了 σ_overall。 Ppk的物理意义:它衡量的是在长期情况下,过程输出的实际表现,同时考虑了长期波动的精度(σ_overall)和过程的准度(μ)。 Ppk是客户最关心的指标之一,因为它反映了你实际交付的产品(包含了所有变异来源)是否符合规格。 第三部分:关键区别与深度对比3.1 Cp/Cpk 与 Pp/Ppk 的根本区别:σ 的不同特征 Cp / Cpk (能力指数) Pp / Ppk (性能指数) σ 的类型 组内标准差 (σ_within) 整体标准差 (σ_overall) 变异来源 主要评估短期、固有的随机变异(普通原因)。 评估长期、总的变异,包含普通原因和特殊原因(如设备磨损、批次差异、操作员变更)。 数据要求 需要分组数据(子组容量>1),通常用于过程稳定性研究(控制图)。 可以使用所有个体数据,不要求分组。常用于初始过程研究或批量产品的验证。 用途 过程改进:评估一个稳定过程的最佳内在潜力。回答“这个过程在受控时能有多好?” 过程验证:评估过程在长期生产中的实际表现。回答“这个过程过去交付的产品总体质量如何?” 比喻 测量一个专业射手在最理想状态下(心情好、无风)打靶的密集度。 测量一个射手在真实战场上(有风、有压力)打靶的总体命中情况。 σ_overall 与 σ_within 的关系: 在理想情况下,σ_within ≈ σ_overall。但在现实中,由于存在子组间的变异,几乎总是 σ_overall > σ_within。因此,对于同一个过程,几乎总是: Pp ≤ Cp 且 Ppk ≤ Cpk 3.2 单边与双边规格双边规格:同时存在 USL 和 LSL。这是最常见的情况,上述四个指数均适用。 单边规格:只有 USL 或只有 LSL。 只有 USL:只能计算 Cpu 或 Ppu,并直接将其作为 Cpk 或 Ppk。 只有 LSL:只能计算 Cpl 或 Ppl,并直接将其作为 Cpk 或 Ppk。 此时 Cp 和 Pp 无法计算(因为分母需要两个规格限)。 第四部分:综合应用与分步指南步骤1:数据收集与准备确定特性:明确要分析的关键质量特性(CTQ)。 收集数据:在足够长的时间范围内收集数据,以捕捉所有可能的变异源。 合理分组:如果计算 Cp/Cpk,需要将数据分成子组(如每小时取5个连续样本)。子组内变异应只来自随机原因,子组间变异可能包含特殊原因。 步骤2:过程稳定性分析(使用控制图)这是计算 Cp/Cpk 的绝对前提! 绘制 Xbar-R 图或 I-MR 图。 如果控制图显示过程不稳定(有点超出控制限或有非随机模式),说明存在特殊原因。必须先找到并消除这些特殊原因,使过程恢复稳定。否则,计算 Cp/Cpk 没有意义,因为过程不具备可预测性。 步骤3:正态性检验过程能力分析(尤其是基于正态分布的百分比估计)假设数据服从或近似服从正态分布。 使用正态概率图或统计检验(如Anderson-Darling)来检查。 如果数据非正态,需要考虑: 进行数据变换(如Box-Cox变换)。 使用非正态过程能力分析(基于其他分布,如韦伯分布、对数正态分布)。 步骤4:选择并计算指数过程是否稳定? 是:可以计算 Cp/Cpk 和 Pp/Ppk。Cp/Cpk 告诉你过程的内在潜力,Pp/Ppk 告诉你当前的实际表现。如果 Pp/Ppk 远小于 Cp/Cpk,说明过程有大量的组间变异未被消除,改进空间巨大。 否:只能计算 Pp/Ppk,因为它描述了过去的总体表现,但不具备预测性。首要任务是使过程稳定。 如何解读结果? 指数值 等级 评价 近似不合格率 (PPM) < 1.0 不足 过程无法满足要求,必然产生不合格品。 > 2700 1.0 临界 过程刚好满足要求,但波动已触及规格限。 ~ 2700 1.33 可接受 有适当的安全边际。对应4σ水平。 ~ 63 1.67 良好 有良好的安全边际。对应5σ水平。 ~ 0.6 2.00 优秀 卓越的过程能力。对应6σ水平。 ~ 0.002 步骤5:解读与行动如果 Cp/Cpk 低: Cp 和 Cpk 都低且相近:主要问题是过程波动太大(σ大)。改进重点在于减小变异(例如,改进设备、材料、方法)。 Cp 尚可但 Cpk 很低:主要问题是过程中心偏离(μ未对准)。改进重点在于调整过程中心至规格中心。 如果 Pp/Ppk 远低于 Cp/Cpk:说明过程存在大量的特殊原因变异(组间变异)。改进重点在于使过程稳定和受控(例如,完善作业标准、加强维护、培训操作员)。 第五部分:总结与核心要点指数 关注的波动 是否考虑中心偏移 主要用途 前提条件 Cp 短期 (Within) 否 评估过程的潜在精度/最佳能力 过程稳定,数据正态 Cpk 短期 (Within) 是 评估稳定过程的实际能力 过程稳定,数据正态 Pp 长期 (Overall) 否 评估过程的整体波动范围 无(描述性统计) Ppk 长期 (Overall) 是 评估过程在长期生产中的实际表现 无(描述性统计) 最终黄金法则: 先稳定,后能力:不稳定的过程计算 Cp/Cpk 是无意义的。 客户看 Ppk:Ppk 反映了你交付的整体质量水平。 改进看 Cpk 和 Cp:它们揭示了过程内在的问题——是位置不准还是波动太大。 差距即机会:如果 Ppk 远小于 Cpk,说明通过过程控制和标准化,有巨大的质量提升和成本节约空间。 还是不够详细,每个参数变量没有详细讲解 好的,我们来对过程能力指数的每一个参数和变量进行原子级别的极致详解。这将是您能找到的最详细的解释。 第零部分:数学符号与函数深度解析0.1 求和符号 Σ (Sigma)全称:大写希腊字母Sigma 含义:求和 数学定义:Σ(Xi) = X₁ + X₂ + X₃ + ... + Xn 计算示例:对于数据集[2, 4, 6, 8] Σ(Xi) = 2 + 4 + 6 + 8 = 20 Σ(Xi²) = 4 + 16 + 36 + 64 = 120 在标准差中的应用:Σ(Xi - μ)² 表示先计算每个数据点与均值的差,平方,再把所有平方值加起来 0.2 最小值函数 min()全称:Minimum Function 含义:从一组数值中返回最小的那个值 数学定义:min(a, b, c, ...) 在Cpk/Ppk中的意义: Cpk = min(Cpu, Cpl) 这体现了木桶原理——过程能力由最差的那一侧决定 哲学意义:一个过程的整体质量水平受限于其最薄弱的环节 第一部分:规格参数的极致详解1.1 USL (Upper Specification Limit) - 上规格限1.1.1 基本定义中文全称:上规格界限/上限规格值 符号表示:USL 物理意义:客户或工程技术要求允许的最大值 数学表达:对于任何合格的产品,必须满足 X ≤ USL 1.1.2 来源与确定方法客户直接指定 例:某孔径要求 10.0 +0.1/-0.0 mm,则 USL = 10.1 mm 工程计算得出 例:某电路电压要求:标称值5V,允许±5%波动 USL = 5 × (1 + 5%) = 5.25V 法规标准规定 例:食品中某重金属含量不得超过2.0 ppm USL = 2.0 ppm 功能边界确定 通过DOE(实验设计)确定产品的功能边界 1.1.3 在公式中的角色在 Cpu = (USL - μ) / 3σ 中: (USL - μ) 代表可用空间——从过程中心到上规格限还有多少距离 这个距离越大,过程产生超差品的风险越小 1.2 LSL (Lower Specification Limit) - 下规格限1.2.1 基本定义中文全称:下规格界限/下限规格值 符号表示:LSL 物理意义:客户或工程技术要求允许的最小值 数学表达:对于任何合格的产品,必须满足 X ≥ LSL 1.2.2 来源与确定方法装配需求 例:轴与孔的配合,轴的直径不能太小 LSL = 标称值 - 公差 性能要求 例:某材料的拉伸强度不得低于500 MPa LSL = 500 MPa 安全考量 例:某安全阀的开启压力不能低于设定值的90% 1.2.3 在公式中的角色在 Cpl = (μ - LSL) / 3σ 中: (μ - LSL) 代表可用空间——从过程中心到下规格限还有多少距离 这个距离越大,过程产生超差品的风险越小 1.3 规格中心 (Nominal/Target Value)1.3.1 基本定义中文全称:规格中心值/目标值 符号表示:通常用 T 或 N 表示 计算公式:T = (USL + LSL) / 2 物理意义:理论上最理想的 process mean 应该所处的位置 1.3.2 重要性在理想过程中,μ = T 当 μ ≠ T 时,即使 Cp 很高,Cpk 也会降低 示例: USL = 10.1, LSL = 9.9 T = (10.1 + 9.9) / 2 = 10.0 如果 μ = 10.05,说明过程中心向上偏移了0.05 第二部分:过程位置参数的极致详解2.1 μ (mu) - 过程平均值2.1.1 基本定义中文全称:过程均值/总体平均值 符号表示:μ (希腊字母mu) 物理意义:过程输出数据的中心位置 2.1.2 详细计算公式总体均值(理论上) μ = (ΣXi) / N Xi:每个个体的测量值 N:总体中的总个体数 样本均值(实践中) x̄ = (Σxi) / n xi:样本中的每个测量值 n:样本容量 x̄ (x-bar) 是 μ 的估计值 2.1.3 计算示例测量5个零件的长度:[10.02, 10.05, 9.98, 10.01, 10.04] mm x̄ = (10.02 + 10.05 + 9.98 + 10.01 + 10.04) / 5 x̄ = 50.10 / 5 = 10.02 mm 2.1.4 在过程能力中的重要性μ 决定了过程的准确度(Accuracy) 当 μ = T 时,过程是"对准的" 当 μ ≠ T 时,过程存在"偏移" 偏移的影响: 即使过程波动很小(σ小),偏移也会导致Cpk降低 偏移是许多质量问题的根源 第三部分:过程波动参数的极致详解3.1 σ (sigma) - 标准差3.1.1 基本概念中文全称:标准差 符号表示:σ (希腊字母sigma) 物理意义:衡量数据相对于均值的离散程度 单位:与原始数据相同的单位 3.1.2 两种标准差的核心区别3.1.2.1 σ_within (组内标准差)定义:仅考虑子组内部的变异,代表过程的短期、固有波动。 计算方法1:通过极差均值估计(最常用) text σ_within = R̄ / d₂参数详解: R̄ (R-bar):子组极差的平均值 极差 R:子组内最大值 - 最小值 计算示例: 子组1:[10.0, 10.1, 10.2] → R₁ = 0.2 子组2:[9.9, 10.0, 10.1] → R₂ = 0.2 子组3:[10.1, 10.2, 10.3] → R₃ = 0.2 R̄ = (0.2 + 0.2 + 0.2) / 3 = 0.2 d₂ 常数:与子组容量相关的统计常数 物理意义:将极差转换为标准差的系数 常用值: 子组大小 n d₂ 值 备注 2 1.128 最常用 3 1.693 4 2.059 5 2.326 工业界最常用 6 2.534 7 2.704 8 2.847 计算方法2:通过子组标准差均值估计 text σ_within = S̄ / c₄参数详解: S̄ (S-bar):子组标准差的平均值 c₄ 常数:与子组容量相关的无偏修正系数 常用值: n c₄ 2 0.7979 3 0.8862 4 0.9213 5 0.9400 3.1.2.2 σ_overall (整体标准差)定义:考虑所有变异来源的长期、总波动。 计算公式: text σ_overall = √[ Σ(xi - x̄)² / (N - 1) ]分步计算示例: 数据:[10, 12, 11, 13, 10] 计算均值:x̄ = (10+12+11+13+10)/5 = 56/5 = 11.2 计算偏差平方和: (10-11.2)² = 1.44 (12-11.2)² = 0.64 (11-11.2)² = 0.04 (13-11.2)² = 3.24 (10-11.2)² = 1.44 Σ = 1.44+0.64+0.04+3.24+1.44 = 6.80 除以(N-1):6.80 / (5-1) = 6.80 / 4 = 1.70 开平方:√1.70 = 1.304 ∴ σ_overall = 1.304 3.1.3 两种标准差的关系与意义特征 σ_within σ_overall 别名 短期标准差、组内标准差 长期标准差、整体标准差 代表变异 随机变异、普通原因 总变异(普通原因+特殊原因) 计算公式 R̄/d₂ 或 S̄/c₄ √[Σ(xi-x̄)²/(N-1)] 在控制图中 通过R图或S图监控 通过单值图反映 过程改进意义 过程的最佳潜力 过程的实际表现 重要关系:在绝大多数情况下: text σ_overall ≥ σ_within当且仅当过程完全稳定且无组间变异时,两者相等。 第四部分:能力指数的分步计算详解4.1 Cp 的计算分解公式:Cp = (USL - LSL) / 6σ_within 计算示例: 已知: USL = 20.5, LSL = 19.5 通过25个子组(n=5)计算得 R̄ = 0.4 d₂ (n=5) = 2.326 分步计算: 计算 σ_within: σ_within = R̄ / d₂ = 0.4 / 2.326 = 0.172 计算 6σ_within: 6σ_within = 6 × 0.172 = 1.032 计算规格宽度: USL - LSL = 20.5 - 19.5 = 1.0 计算 Cp: Cp = 1.0 / 1.032 ≈ 0.97 解读:Cp < 1,说明即使过程完美居中,其固有波动也已经超出了规格范围。 4.2 Cpk 的计算分解公式:Cpk = min(Cpu, Cpl) 继续上例,假设测得过程均值 μ = 20.1 分步计算: 计算 Cpu: Cpu = (USL - μ) / 3σ_within = (20.5 - 20.1) / (3 × 0.172) = 0.4 / 0.516 ≈ 0.78 计算 Cpl: Cpl = (μ - LSL) / 3σ_within = (20.1 - 19.5) / (3 × 0.172) = 0.6 / 0.516 ≈ 1.16 计算 Cpk: Cpk = min(0.78, 1.16) = 0.78 深度分析: Cp = 0.97:过程潜力尚可 Cpk = 0.78:实际能力不足 根本原因:过程中心向上偏移(μ = 20.1 > 目标值20.0) 改进方向:调整过程中心,使其向目标值20.0靠近 4.3 常数"3"和"6"的深层含义4.3.1 3σ 的统计意义在正态分布中,μ ± 1σ 包含68.27%的数据 μ ± 2σ 包含95.45%的数据 μ ± 3σ 包含99.73%的数据 因此,6σ 代表了过程的自然公差范围 4.3.2 为什么用 3σ 而不是 2σ 或 4σ?历史原因:由休哈特博士在1920年代提出,已成为工业标准 实用考量:3σ在敏感度和经济性之间取得平衡 质量水平:3σ对应2700 PPM(百万分之缺陷数),是工业界的基准水平 第五部分:综合对比与决策矩阵5.1 四大指数的完整对比指数 分子 分母 考虑中心? 标准差类型 用途 Cp USL-LSL 6σ_within ❌ 短期 过程潜力 Cpk min(到USL,到LSL) 3σ_within ✅ 短期 实际短期能力 Pp USL-LSL 6σ_overall ❌ 长期 整体波动 Ppk min(到USL,到LSL) 3σ_overall ✅ 长期 实际长期表现 5.2 诊断矩阵:如何根据指数值判断问题Cp vs Cpk 模式 问题诊断 改进方向 Cp ≈ Cpk 且都高 过程优秀 维持现状 Cp ≈ Cpk 且都低 波动太大 减小变异 Cp 高但 Cpk 低 中心偏移 调整过程均值 Pp ≪ Cp 特殊原因变异多 使过程稳定 5.3 行业标准要求行业 最低要求 良好水平 优秀水平 一般制造业 Cpk ≥ 1.33 Cpk ≥ 1.67 Cpk ≥ 2.0 汽车行业 Cpk ≥ 1.33 Cpk ≥ 1.67 Cpk ≥ 2.0 航空航天 Cpk ≥ 1.50 Cpk ≥ 2.0 Cpk ≥ 2.5 半导体 Cpk ≥ 1.67 Cpk ≥ 2.0 Cpk ≥ 2.5 还有不懂的吗?
在手机APP中查看
更方便的浏览方式。了解更多信息。
_b9b0b7.png)
_6cf02d.png)
_6d4f93.png)
_77267e.png)